分部和分——阿贝尔变换
在离散领域也有“分部积分”(Integration by parts)公式,不妨称之为“分部和分”(Summation by parts)。这一公式又被称为“阿贝尔变换”,得名于其作为推导无穷级数的敛散性判定准则的一个重要引理。
定理
已知数列\(\{a_n\},\{b_n\}\),\(\{\Delta a_n\}\)是\(\{a_n\}\)的一阶后向差分(\(\Delta a_n = a_{n} - a_{n-1}\),特别地,定义\(\Delta a_1 = a_1\)),\(\{B_n\}\)是\(\{b_n\}\)的前\(n\)项和。那么离散和\(\sum_{i=1}^n a_ib_i\)的阿贝尔变换是指
\[ \sum_{i=1}^n a_ib_i = a_nB_n -\sum_{i=1}^{n-1} \Delta a_{i+1}B_i. \tag{*} \]
证明从略。但上式看上去可一点也不像分部积分?不妨“换元”试试。记\(\{\Delta b_n\}\)是\(\{b_n\}\)的一阶差分,那么\(\{b_n\}\)就是\(\{\Delta b_n\}\)的前\(n\)项和。我们将上述两个“换元”代入上式,得
\[ \sum_{i=1}^n a_i \Delta b_i = a_nb_n- \sum_{i=1}^{n-1} b_i \Delta a_{i+1}. \tag{**} \]
这十分接近于分部积分的公式
\[ \int u \, \mathrm{d}v = uv - \int v \, \mathrm{d}u. \]
另外,使用一阶前向差分也可以定义阿贝尔变换,两者是等价的。
在使用阿贝尔变换时,也可以使用分部积分的表格法,但相对分部积分有如下几点变化:
- \(u\)行从微分计算变成了差分计算,\(v\)行从积分计算变成了和分计算
- \(v\)行需要动态调整当前求和计算的上界,并注意\(u\)行所需代入的为第\(n-i\)项。
具体情况详见下文的表格。
阿贝尔判别法
若\(\{a_n\}\)单调有界,且\(\sum b_n\)收敛,则\(\sum a_nb_n\)收敛。
狄利克雷判别法
若\(\{a_n\}\)单调递减趋于\(0\),且\(\{b_n\}\)的部分和有界,则\(\sum a_nb_n\)收敛。
阿贝尔变换如果仅仅作为一个推导无穷级数的敛散性判定准则的引理,未免也太可惜了——让我们看看如何利用阿贝尔变换进行数列求和吧。
应用
- 求数列\(\{n\cdot 2 ^{n-1}\}\)的前\(n\)项和。
解答 令\(a_n=n,b_n=2^{n-1}\),则由\((*)\)式知,所求
\[ \sum_{i=1}^n a_ib_i = a_nB_n -\sum_{i=1}^{n-1} \Delta a_{i+1}B_i. \]
其中
\[ B_n = \sum_{i=1}^n 2 ^{i-1} = 2^n-1, \\ \Delta a_{i+1} = 1, \]
故
\[ \sum_{i=1}^n a_ib_i = n(2^n-1) - \sum_{i=1}^{n-1} (2^i - 1) = n(2^n-1) - (2^n-n-1) = (n-1)2^n + 1. \]
表格
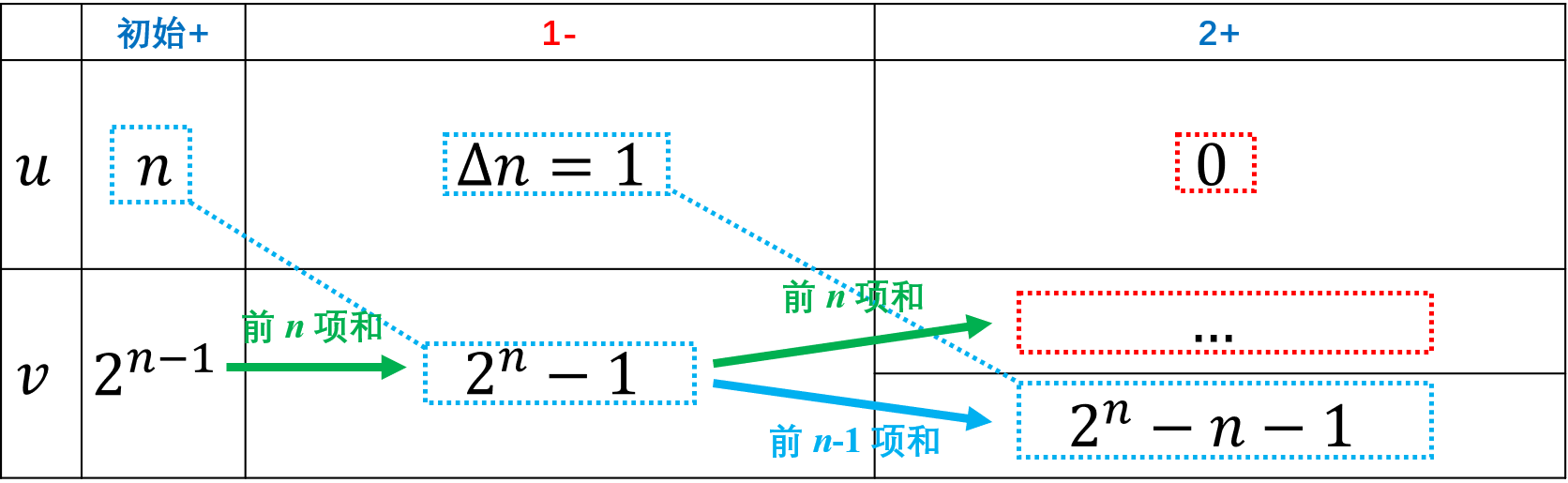
\[ \begin{aligned} \sum_{i=1}^n i \cdot 2^{i-1}&= n(2^n - 1) - 1 \cdot (2^n - n - 1) + \sum_{i=1}^{n-2} 0 \cdot \left( \sum_{j=1}^{i} (2^j - 1) \right) \\ &= n(2^n - 1) - 1 \cdot (2^n - n - 1) \\ &= 2^n(n-1) + 1. \end{aligned} \]
- 求数列\(\{n^2 \cdot 2^n\}\)的前\(n\)项和。
解答 令\(a_n=n^2,b_n=2^{n}\),仍然
\[ B_n = 2(2^n-1), \\ \Delta a_{i+1} = (n+1)^2-n^2 = 2n+1. \]
故
\[ \sum_{i=1}^n a_ib_i = 2n^2(2^n-1) - \sum_{i=1}^{n-1} 2(2i+1)(2^i-1), \]
对\(\sum_{i=1}^{n-1} 2(2i+1)(2^i-1)\)再使用一次阿贝尔变换(注意求和上限变成了\(n-1\)),经过不小的计算量得到
\[ 2\sum_{i=1}^{n-1} (2i+1)(2^i-1) = 2\left((2n-1)(2^n-1-n) - \sum_{i=1}^{n-2} (2)(2^{i+1}-i-2)\right) = 2 (-n^2+2^{n+1} n-3 \cdot 2^n+3). \]
于是
\[ \sum_{i=1}^n a_ib_i = 2 (2^n n^2-2^{n+1} n+3\cdot 2^n-3) = 2^{n+1}(n^2-2n+3) - 6. \]
表格
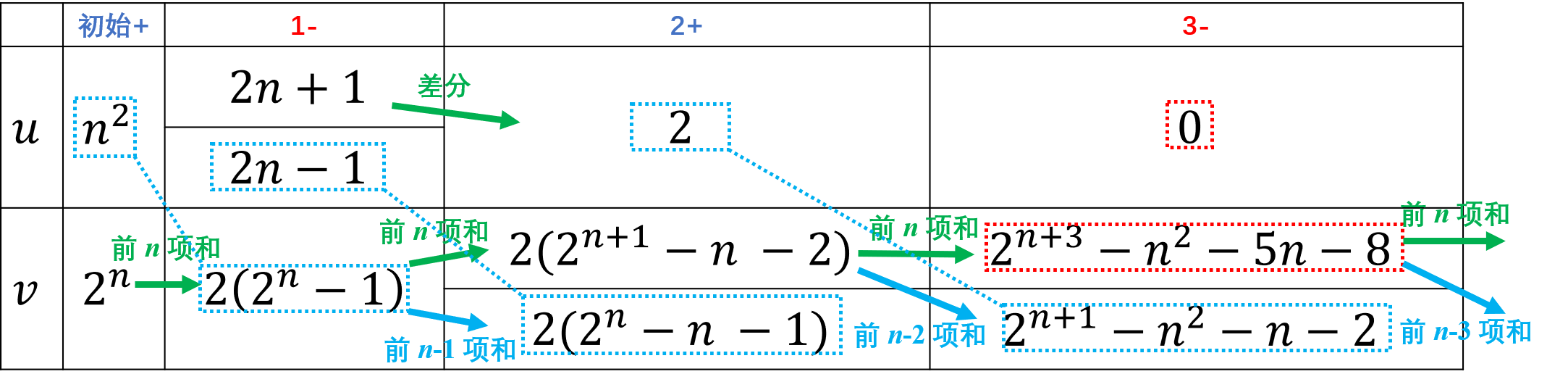
\[ \begin{aligned} \sum_{i=1}^n i^2 2^i &= n^2 \cdot 2(2^n - 1) - (2n-1)2(2^n-n-1)+2(2^{n+1}-n^2-n-2) - \sum_{i=1}^{n-3} 0 \cdot (2^{i+3} - i^2 - 5i -8) \\ &= n^2 \cdot 2(2^n - 1) - (2n-1)2(2^n-n-1)+2(2^{n+1}-n^2-n-2) \\ &= 2^{n+1}(n^2-2n+3) - 6. \end{aligned} \]
- 求\(S_n = \sum_{i=1}^n i^2\)。
解答
设\(u=v=n\),那么
\[ S_n = n \cdot \frac{n(n+1)}{2} - \frac{1}{2} \left (S_{n-1} + \frac{n(n-1)}{2} \right), \]
其中\(S_n - S_{n-1} = n^2\)。解得\(S_n = \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}\)。
事实上,可以直接待定一个\(k+1\)次多项式的系数,来求形如\(\sum_{i=1}^n i^k\)的通项。
- 表格演示\(\sum_{i=1}^n i^3\),取\(u=n^3, v= 1\)时的计算。
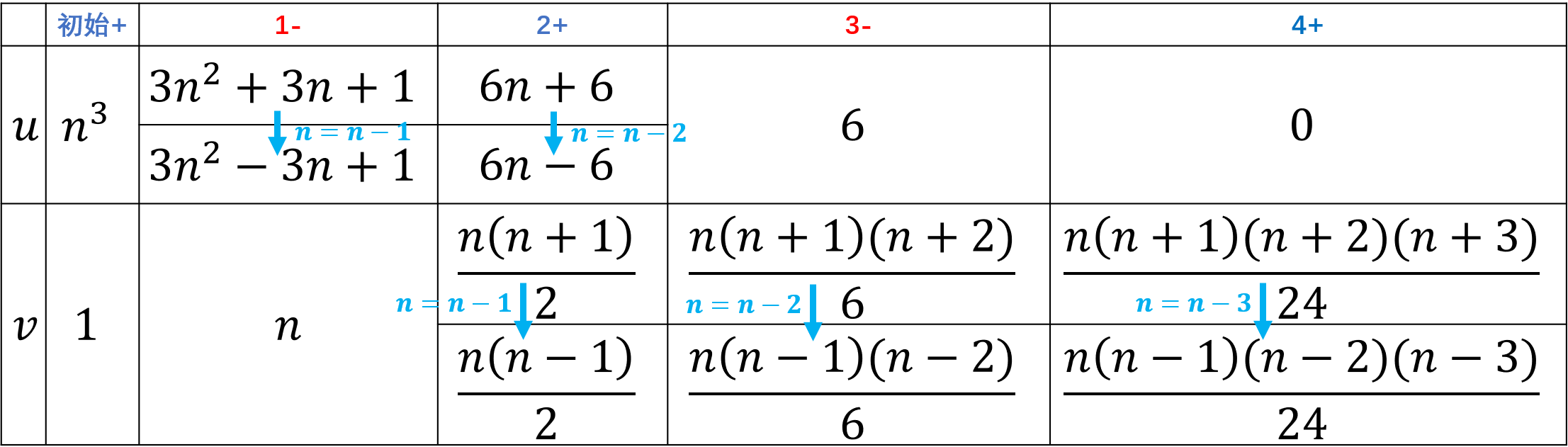
\[ \sum_{i=1}^n i^3 = n^3 \cdot n - (3n^2-3n+1)\left(\frac{n(n-1)}{2} \right) + (6n-6)\left(\frac{n(n-1)(n-2)}{6} \right) - 6\left(\frac{n(n-1)(n-2)(n-3)}{24} \right) \]
这个表格的和分部分相当有趣:它告诉我们,对\(n\)连续做和分运算的结果
\[ \frac{n(n+1)}{2!}, \\ \frac{n(n+1)(n+2)}{3!}, \\ \frac{n(n+1)(n+2)(n+3)}{4!}, \]
与对\(x\)连续做积分运算的结果
\[ \frac{x^2}{2!}, \\ \frac{x^3}{3!}, \\ \frac{x^4}{4!}, \\ \]
形成了一一对应。
- 记\(S_n = \sum_{i=1}^n \frac{H_i}{i(i+1)}\),其中\(H_i = \sum_{j=1}^i \frac{1}{j}\)。求\(\lim_{n \to \infty} S_n\)。
https://www.bilibili.com/video/BV1JW4y1U7NF
解答
发现分子适合差分,分母适合和分,于是令\(u=H_n, v = \frac{1}{n(n+1)} = \frac{1}{n} - \frac{1}{n+1}\),运用一步分部和分,得到
\[ \begin{aligned} S_n &= H_n \left(1 - \frac{1}{n+1} \right) - \sum_{i=1}^{n-1}\left(1 - \frac{1}{i+1} \right)\left(\frac{1}{i+1} \right) \\ &= H_n \left(1 - \frac{1}{n+1} \right) - \sum_{i=1}^{n-1}\frac{1}{i+1} + \sum_{i=1}^{n-1}\frac{1}{(i+1)^2} \\ &= H_n \left(1 - \frac{1}{n+1} \right) - (H_n - 1) + \sum_{i=1}^{n-1}\frac{1}{(i+1)^2} \\ &= -\frac{1}{n+1}H_n + 1 + \sum_{i=1}^{n-1}\frac{1}{(i+1)^2} \\ &= \sum_{i=1}^{n}\frac{1}{i^2} -\frac{1}{n+1}H_n. \end{aligned} \]
故\(\lim_{n \to \infty} S_n = \sum_{n=1}^{\infty}\frac{1}{n^2} = \frac{\pi^2}{6}\)。
经过验证,发现在计算前\(n\)项和时,该方法与错位相减法相比,计算量并没有显著减少,因此笔算实用性不高,但程序计算实用性较高。当然,这个数列求和方法很适合熟悉分部积分表格法的同学。