最小圆覆盖问题
给定一个\(n\)顶点的二维多边形,以每个顶点为圆心作一个半径为\(r\)的圆,记第\(i\)个顶点对应的圆覆盖的区域为\(R_i\)。求使得\(\bigcup_{i=1}^n R_i\)覆盖整个多边形内部区域的最小半径\(r^*\)。
图例
下图的半径\(r\)不足以覆盖多边形内部区域:
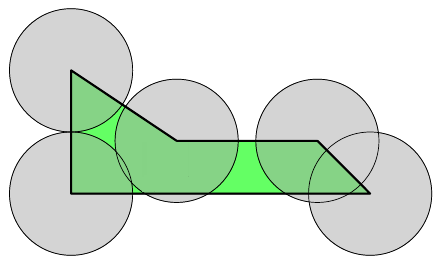
下图的半径\(r^*\)是足以覆盖多边形内部区域的最小半径:
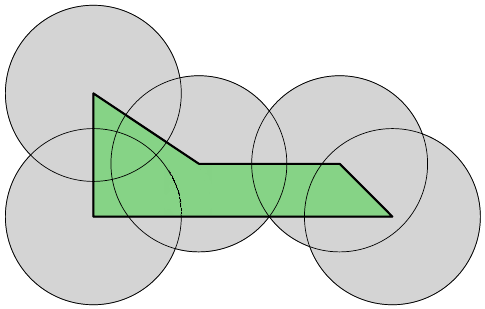
解答
首先,该问题存在一个对半径\(r\)进行二分查找,并在多边形内进行采样以输出覆盖可行性的算法。该算法依赖一定的采样流程,难以求出精确的\(r^*\),效率也不高。下文将介绍用Voronoi图作为数据结构的高效算法。
记多边形的各顶点组成的集合为\(S = \{\mathbf p_1, \dots, \mathbf p_n\}\),多边形内部区域(包含边界)为\(P\),\(\mathbf p \in P\)是多边形内部的任意点。当\(r < r^*\)时,总存在\(\mathbf p\),满足\(\forall i, ||\mathbf p - \mathbf p_i|| > r\),即所有顶点对应的圆无法覆盖到该点。当\(r\)不断增大,直到当\(r = r^*\)时,上不等式对至少一个\(i\)取等,即存在临界点\(\mathbf q \in P\)恰好在第\(i\)个顶点的圆上,\(\exists i, ||\mathbf q - \mathbf p_i|| = r^*\),且对于其他\(j \neq i\)有\(||\mathbf q - \mathbf p_j|| \geq r^*\)。
容易发现,这样的临界点\(\mathbf q\)最大化了到\(S\)中各点的最小距离,且这个距离就是我们要求的\(r^*\)。考虑为\(S\)建立Voronoi图,并通过各生成点\(\mathbf p_i\)对应的Voronoi区域\(R^=(\mathbf p_i)\)对\(P\)进行区域划分,由此我们获得了多边形内的若干区域,如下图所示:
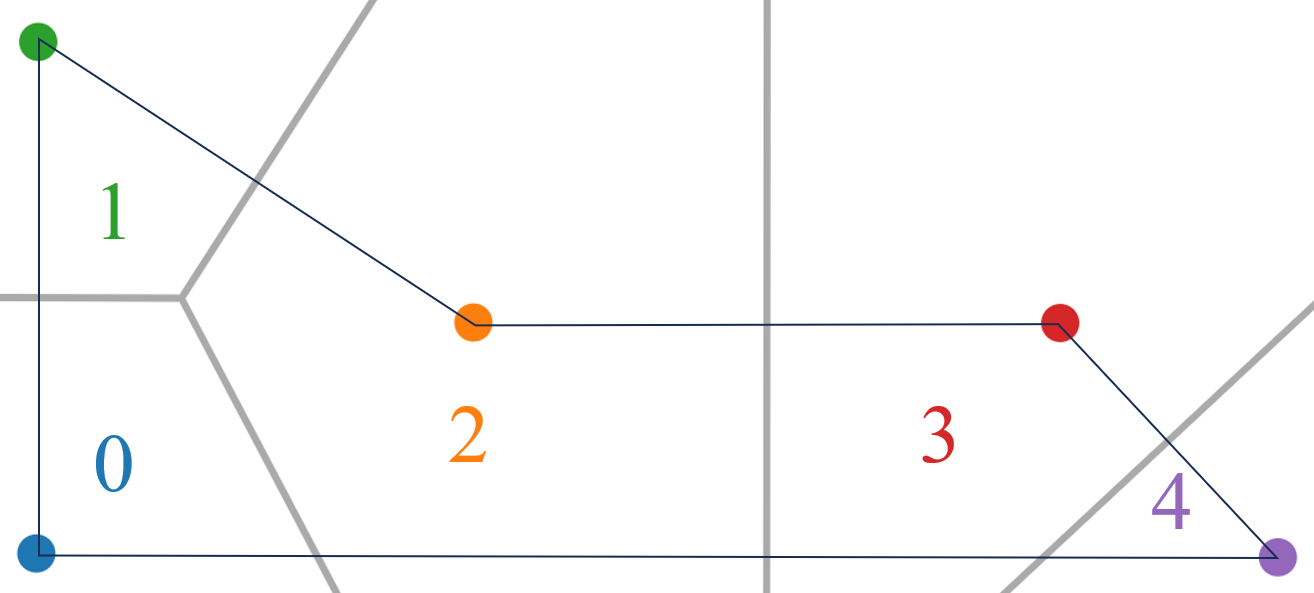
临界情况如下图所示:
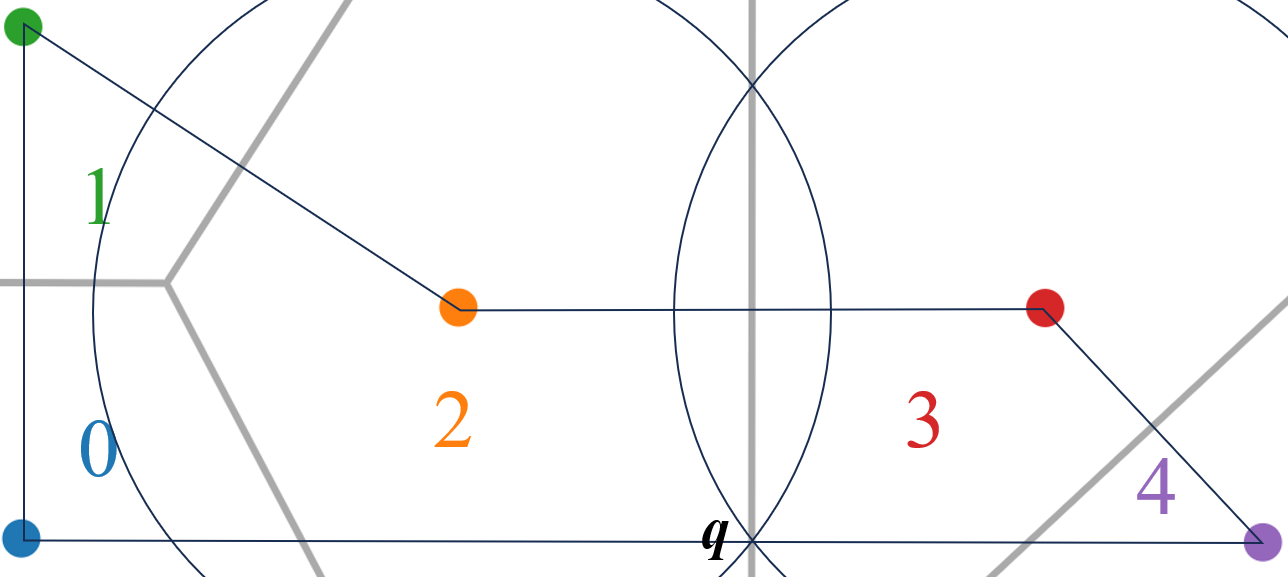
那么,\(\mathbf p \in P\)到\(S\)中各点的最小距离完全由\(\mathbf p\)所处的Voronoi区域决定——若\(\mathbf p \in R^=(\mathbf p_i) \cap P\),则该距离的值为\(||\mathbf p_i - \mathbf p||\)。于是,我们只需枚举所有\(\mathbf p_i\),然后枚举区域\(R^=(\mathbf p_i) \cap P\)内的点,最大化\(||\mathbf p_i - \mathbf p||\)即可。
于是,我们将原问题转化为了如下的优化问题:
\[ \max_{i} z(\mathbf p_i) \ \ \ s.t. \begin{cases} z(\mathbf p_i) = \max_{\mathbf p}(||\mathbf p_i - \mathbf p||), \\ \mathbf p \in R^=(\mathbf p_i) \cap P. \end{cases} \]
对给定的\(\mathbf p_i\),如何最大化\(||\mathbf p_i - \mathbf p||\)?注意到区域\(R^=(\mathbf p_i) \cap P\)必然为多边形,可以用圆扩张的思想证明,一个多边形上的顶点\(\mathbf p_i\)与多边形内部(或边界)一点\(\mathbf p\)的最大距离,一定在\(\mathbf p\)位于多边形的(另一)顶点时取到。于是,我们不需要在二维区域\(R^=(\mathbf p_i) \cap P\)上枚举\(\mathbf p\),只需遍历有限的\(R^=(\mathbf p_i) \cap P\)的顶点,取最大化距离的\(\mathbf p\)即可。
于是,算法的步骤可以如下描述:
- 在多边形顶点集\(S\)上建立Voronoi图。
- 对多边形的每个顶点\(\mathbf p_i\),取多边形\(R^=(\mathbf p_i) \cap P\)的顶点集\(T_i\)。\(T_i\)中包含三种顶点:原多边形的顶点(也可忽略,不影响答案)、Voronoi点,以及原多边形的边与Voronoi边的交点。
- 遍历\(\mathbf p \in T\),计算\(||\mathbf p_i - \mathbf p||\);若计算结果大于当前最大值,则更新答案。若\(T_i\)遍历完毕,\(i = i + 1\)并回到步骤(2)。
可以证明,对给定的\(\mathbf p_i\),多边形\(R^=(\mathbf p_i) \cap P\)的顶点集\(T_i\)的平均规模为\(O(n)\),而原多边形顶点集\(S\)的规模为\(O(n)\),故算法的整体时间复杂度为\(O(n^2)\)。
更进一步地观察可以发现,临界点仅会在所有Voronoi点或原多边形的边与Voronoi边的交点上取到,因此可以直接枚举两种点:
- 枚举Voronoi点\(\mathbf p\)时,再枚举\(\mathbf p_i\),计算\(||\mathbf p_i - \mathbf p||\),更新答案,时间复杂度\(O(n^2)\)。
- 枚举原多边形的边与Voronoi边的交点时,计算交点花费\(O(n^2)\)时间;然后对每个交点\(\mathbf p\),取其所在Voronoi边垂直平分的\(S\)中顶点\(\mathbf p_i, \mathbf p_j\),计算\(||\mathbf p_i - \mathbf p||\)或\(||\mathbf p_j - \mathbf p||\),更新答案,花费\(O(1)\)时间。例如,图例中的临界点\(\mathbf q\)就是这样的点,只需计算其与\(\mathbf p_2\)或\(\mathbf p_3\)的距离即可。
算法整体时间复杂度仍为\(O(n^2)\),但简化了一些共享顶点的重复计算和求交流程。